投資では「複利」「長期」「分散」が重要だといわれています。
しかし、これは本当なのでしょうか?
この根源的な質問に関して、先人の研究の成果を参考にしつつ解明し、投資についての素人にもわかりやすい説明を加えることに挑戦してみたい思います。
「長期投資ほどリスクは低くなる」とよく言われています。
この意味について考えてみます。
あえて正確さを無視して平易に表現すれば、このようになります。
長い期間のリスク(ブレ)の平均値は、期間が長ければ長いほど平均化されて安定していきます。
このことをもって長期ほどリスクが低いといわれています。
しかしながら常識に立ち返って考えてみれば、向こう1年間についてよりも向こう30年間についての方が不確実性が高まるということは感覚的に理解できるのではないかと思います。
つまり長期ほどブレの大きくなる可能性は高まります。
一つ例を挙げて説明します。
例えばドル円の為替レートです。
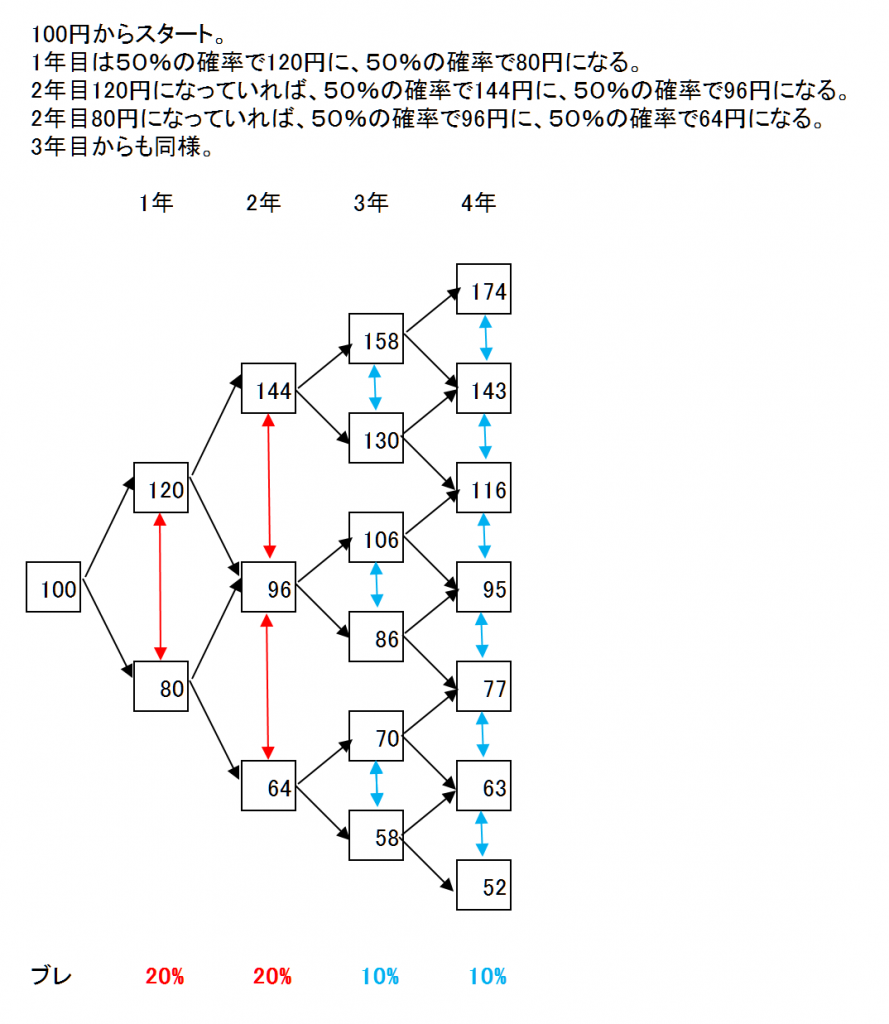
100円からスタートして、1年目は20%のブレ、2年目も20%のブレ、3年目は10%のブレ、4年目は10%のブレだとします。
1年間だけ見ると年間のブレは20%のブレだったり10%のブレだったりブレにばらつきがあります。
しかし、4年間の平均の年間ブレは(20+20+10+10)÷4=15%となり平均化されてくる。
1年間だけだと10%ぶれるのか20%ぶれるのかわからないので不確実性は高い。
しかし、4年間の平均をとると15%のブレになるので1年間だけの時に比べると不確実性は低くなる。
このことを「長期投資ほどリスクは低くなる」と言っているのに過ぎないのです。
投資をする人の立場から考えれば、1年間のブレの話よりも最終的な投資成果(金額)がどうかに関心があります。
1年間だけだと80円から120円の間のいくらかになっています。
4年間経つと52円から174円の間のいくらかになっていることになります。
長期間であればあるほど、もの凄く儲かっているかもしれないしものすごく損しているかもしれないということになります。
長期投資の方がリスクが高いといったほうが投資する人の感覚にマッチするし、誤った判断につながらないのではないでしょうか。
リスクの定義をどのようにするかということかもしれません。
このことを少し難しく専門的に言うと以下のようになります。
表1 投資期間の違いによるリスク指標の違い
|
投資期間(年)
|
||||
|
1
|
5
|
10
|
20
|
|
| 年間標準偏差σ (%) |
20.00
|
20.00
|
20.00
|
20.00
|
| 累積リターン標準偏差σ √T (%) |
20.00
|
44.72
|
63.25
|
89.44
|
| 年率リターン標準偏差σ √T (%) |
20.00
|
8.94
|
6.32
|
4.47
|
| 損失確率N (-0.1/σ) (%) |
30.85
|
13.18
|
5.69
|
1.27
|
| 1/1,000 の確率で失う資産の比率 (%) |
40.50
|
58.43
|
61.48
|
73.92
|
参照: マーク・クリッツマン『資産運用の常識・非常識』
年率リターンの標準偏差は年間標準偏差に投資期間(年)の平方根を掛けて投資期間(年)で割ったものです。
この数字は投資期間が長くなればなるほど小さく(1年で20%であれば、20年では4.47%)なるのは当然です。
しかし、この数字をもって長期投資ほどリスクが小さいと言っていいのでしょうか?
この数字が小さいということは、投資をする人にとってほとんど何の意味も持たないのではないでしょうか。
投資をする人にとって最大の関心の的はこの数字が小さいことよりも、むしろ20年経過した時点での累積の投資成果がどうかということではないでしょうか。
言い換えれば、1年経過した時と20年経過した時を比べて、後者の方が①一番起こりそうな運用結果(金額)が大きいのか、同様に後者の方が②期待リターンでの複利運用結果(金額)になる確率が高いか、更に同様に後者の方が③元本割れの確率が低いのか、といったことの方が重要なのではないでしょうか?
大変残念なことなのですが、今あげた3つの重要関心事については以下にお示しする例では短期に比べて長期の方が悪い数字となっています。
別の回にお話ししますが、リスクを適切にコントロールしないとこのような結果になってしまいます。
年率リターンの標準偏差が投資期間が長いほど小さいということをもって、「長期ほど投資のリスクが低くなる」と表現し投資をする人に伝えることは、上記①②③について長期ほどよい数字になるという誤った印象を与えてしまうのではないでしょうか。
現在の標準的な投資理論に基づいて、標準偏差(リスク)と投資期間の異なる投資について、少し極端な条件の下でリターンとリスクの関係をシミュレーションしてみた結果を以下に掲示します。
【前提条件】
投資金額 :100万円
投資期間 :1年間と30年間
期待リターン :5%
標準偏差(リスク):15%と30%
|
標準 |
15% | 30% | 複利運用 結果 |
||||
| 投資 期間 |
一番起こり |
期待リターンでの複利運用結果の 確率 |
元本割れの 確率 |
一番起こり そうな 運用結果 |
期待リターンでの複利運用結果の 確率 |
元本割れの 確率 |
|
| 1年 | 101.9万円 (年率1.9%) |
47.2% | 39.3% | 93.3万円 (年率▲6.7%) |
44.4% | 48.6% | 105万円 |
| 30年 | 174.1万円 (年率1.9%) |
34.9% | 6.8% | 12.6万円 (年率▲6.7%) |
22.1% | 42.6% | 432.2万円 |
いかがでしょうか。
この数字の評価については次回お伝えしたいと思います。
この記事のシリーズを最後まで読んでいただくことによって、投資に関する本によく出てくる以下のようなグラフが本当に正しいのかについても理解いただけるでしょう。
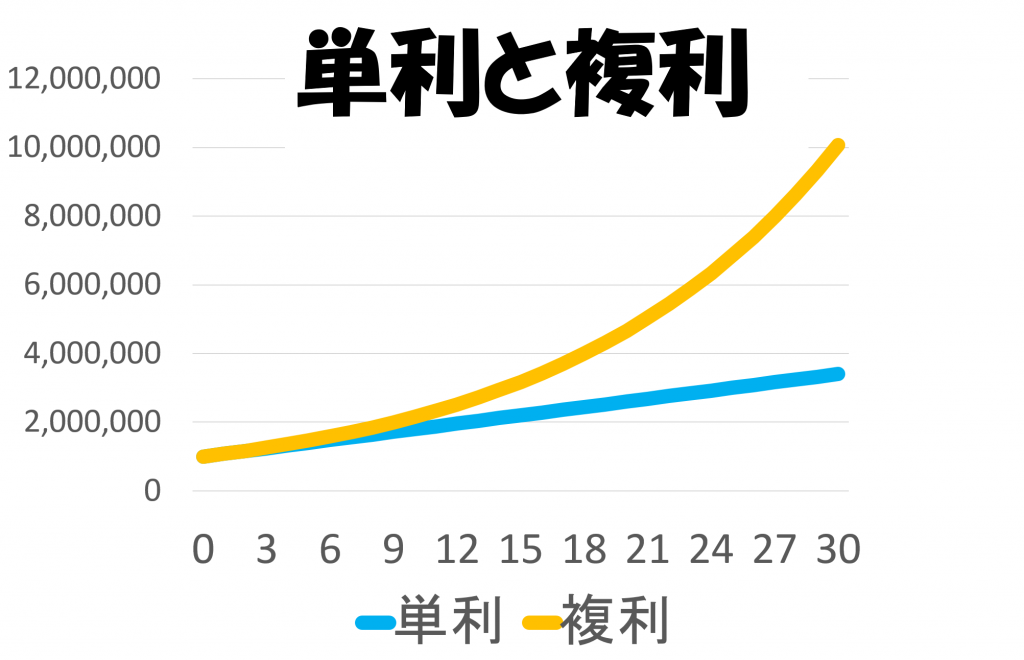
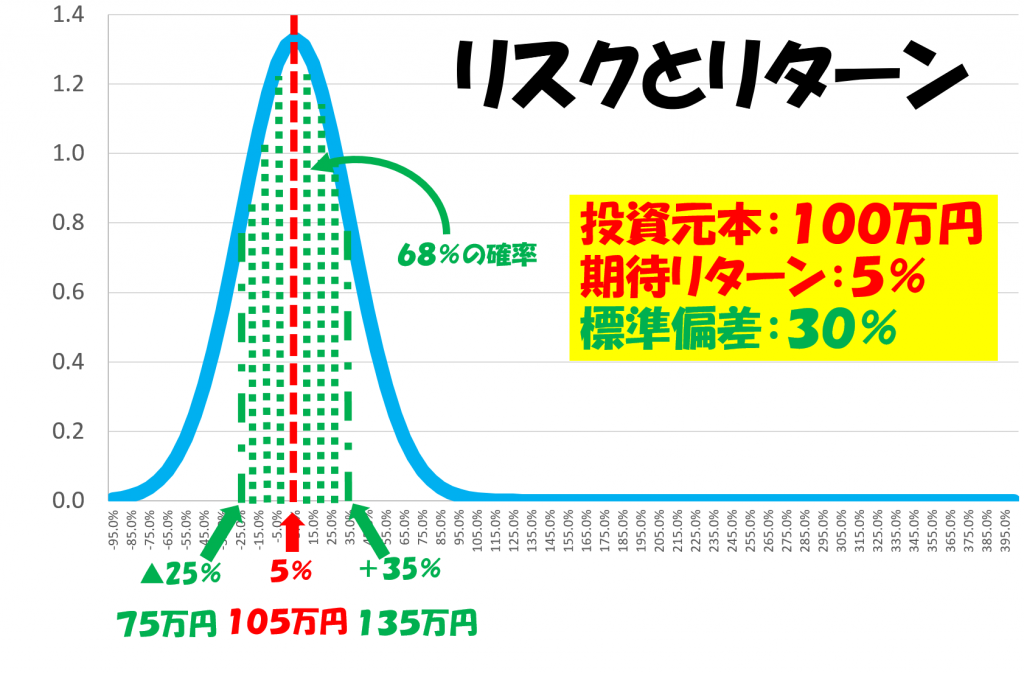
お楽しみに!
【参考サイト】
この分野に関しては、すばらしい先人の研究があります。
ありがとうございます!!!
正確ながらもわかりやすいという点でこれらの先人の研究を超えられるかが、今回の私の挑戦です。
<ファンドの海>
http://www.fund-no-umi.com/blog/2009/05/16-6227.html
<高橋文郎のページ>
http://www.e-takahashi.net/management/management212.html
<山崎元「ホンネの投資教室」>
https://www.rakuten-sec.co.jp/web/market/opinion/yamazaki/yamazaki_20130621.html
<ひと手間加えた積立投資で資産形成>
http://valavg.com/risk-return-compound-1/