「ハイリスク・ハイリターン」といわれているのに、
「同じリターンでリスクを下げる」なんてことできるの?
「連続複利収益率が正規分布する」が現在のポートフォリオ理論の標準的な原則となっています。
つまり、とんがった富士山のような分布ということです。
このことから導き出される長期の場合の投資成果(リターン、金額)は正規分布とは似ても似つかないようなかなり平坦なものになり、リスクが高いと山が左の(投資成果の小さい)方に、逆にリスクが低いと山が右の(投資成果の大きい)方にずれていくことがわかりました。
シミュレーションでは、リスクが30%の場合に比べ15%の場合は山(確率の高いところ)が右の方にずれ、
①一番起こりそうな運用結果(最頻値)
②元本額を割る確率
③期待リターン複利で運用できる確率
のいずれについても劇的に改善していました。
長期投資を救うスーパーマン、「低いリスク」に出会うことができました。
しかし、リスクとリターンは裏腹の関係。
ハイリスク・ハイリターンということから、同じリターンで低いリスクなんて無理なんじゃないのか、という大きな壁に直面しました。
さあ、同じリターンで低いリスクが可能なのか、が今回のテーマです。
リスクとリターンの関係に大きな影響を与えるのが、「相関」というものです。
あまり面白くないかもしれませんが、凄いことを知るための準備。
しばし我慢を。
下の図をご覧ください。
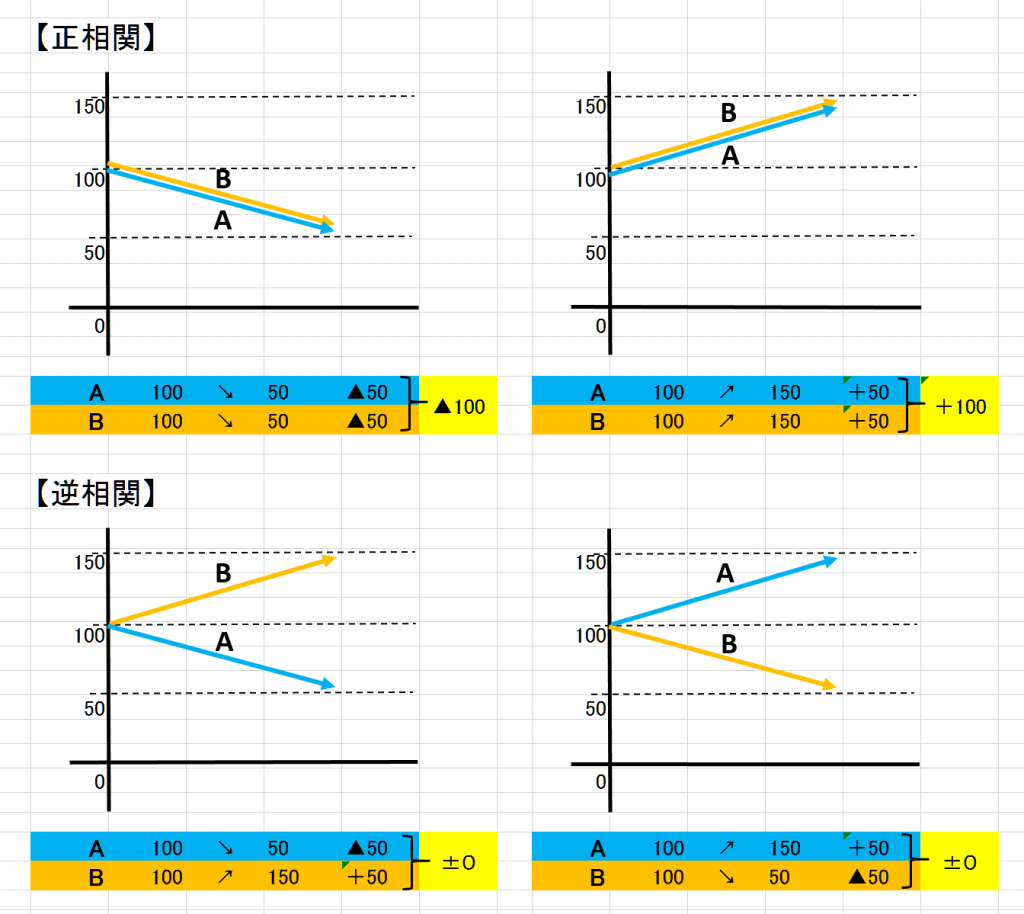
商品Aと商品Bの価格の動きが同じとき(正相関)には、商品Aの価格が下がれば商品Bの価格も下がり、損失は2倍になります。
同じ正相関の場合、逆に商品Aの価格が上がれば商品Bの価格も上がり、利益が2倍になります。
商品Aと商品Bの価格の動きが正反対のとき(逆相関)には、商品Aの価格が下がれば商品Bの価格は上がり、損益は±ゼロになります。
同じ逆相関の場合、逆に商品Aの価格が上がれば商品Bの価格は下がり、損益は±ゼロになります。
このように、価格の動きが逆になるものを組み合わせると損益が相殺され、大きな損失や大きな利益になりにくくなります。
言い換えれば、リスクを小さくすることができます。
価格の動きの方向性が異なるものを適切に組み合わせることにより、リスクを低くくすることができるのです。
以上が価格の動きの方向性の異なる商品を組み合わせるとリスクを下げることができるということのザックリとした説明です。
次に、もう少し詳しくシミュレーションしてみましょう。
まず、相関係数です。
商品Aと商品Bが全く同じ動きをするとき、相関係数は1となります。
逆に全く逆の動きをするときは、相関係数は▲1です。
相関係数は▲1~1までの間の数値を取ります。
二つの商品を組み合わせた場合のリターンとリスクの計算方法は以下の通りです。
| リターン | リスク | |
| 資産A | 2% | 5% |
| 資産B | 4% | 10% |
| 資産Aと資産Bの相関係数 | 0.3 |
| 資産A と 資産B の割合 | 70%:30% |
【リターン】
単純な加重平均です。
0.02 × 0.7 + 0.04 × 0.3 = 0.026 ⇒ 2.6%
【リスク】
ちょっと面倒です。
0.7² × 0.05² + 0.3² × 0.1²
+ 2 × 0.7 × 0.05 × 0.3 × 0.1 × 0.3 = 0.002755
√0.002755 = 0.052488 ⇒ 5.2488%
※0.7² は0.7の2乗の意味。
さあ、準備が整いました。
ここから先には、今までの常識を覆すような面白い世界が待っています。
しばらく期間を開けてから再開したいと思います。
またお会いするのを楽しみにしています。